Excel und Matrixformeln

Formules matricielles - premiers exercices

Premier exercice simple: Somme des nombres 1 à n

Pour illustrer la puissance nous formons la somme des nombres 1 à n. Nous pourrions nous servir de la formule n·(n+1)/2, mais l'exercice sert à montrer ce dont les formules matricielles sont capaples.

Variante A

Nous commençons en saisissant la formule '=Ligne()' dans la colonne Spalte "A" pour générer la séquence des nombres naturels de 1 à 40'000. Dans la cellule "C3" nous calculons la somme au moyen d'une référence à la plage: '=SOMME(DECALER(A1;0;0;40000))'

Nous enregistrons le classeur et constatons une taille de fichier (en Office 2016) d'envion 442 KO.

Variante B

Nous remplaçons la formule en colonne "A" par les valeurs et sauvegardons une copie du classeur sous un autre nom et trouvons une taille de fichier de 333 KO

Variante C

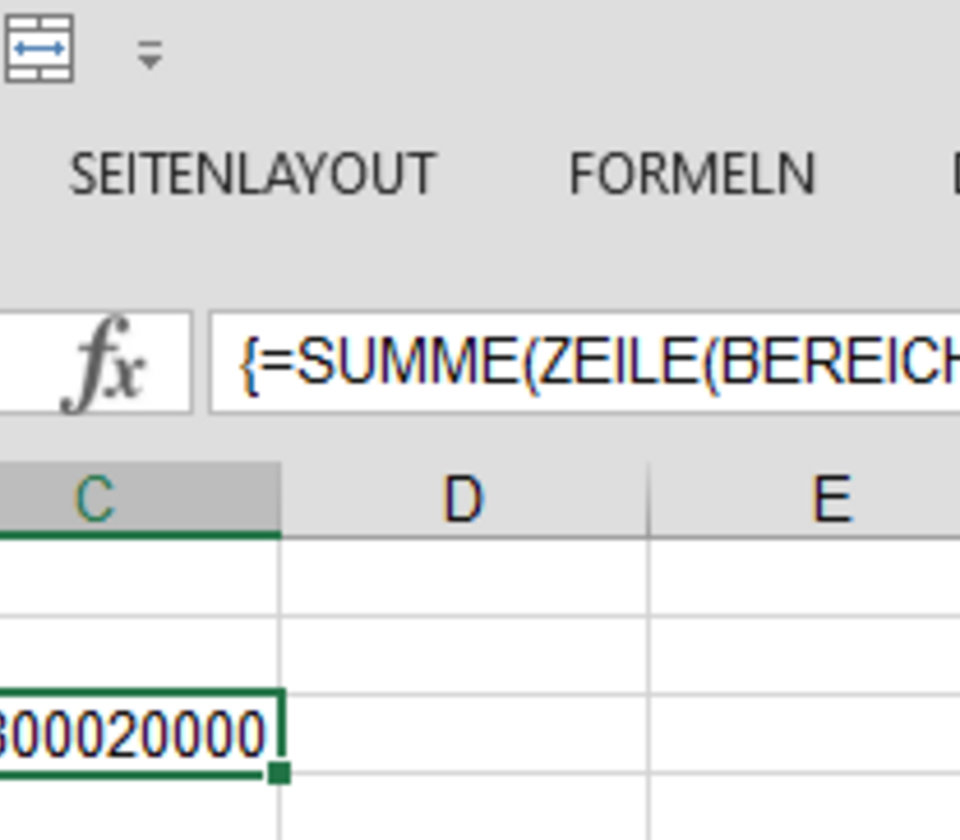
Pour illustrer la construction de la formule matricielle, nous générons, dans un premier pas, dans la colonne "A", les valeurs de 1 à 40000 à l'aide d'une formule matricielle. Pour ce faire, nous sélectionnons la plage englobant toutes les valeurs (c.-à-d. la plage "A1:A40000") et saisissons dans le champ de saisie : '=LIGNE(DECALER(A1;0;0;40000))'

Nous validons la saisie en appuyant sur "Ctrl"+"Maj"+"Valdier", ce qui désigne la formule de nature matricielle. En sélectionnant n'importe quelle cellule de la plage, la formule est affichée en accolades : '{=LIGNE(DECALER(A1;0;0;40000))}'. Sauvegerdé, ce classeur a la même taille que celui de la Variante A.

Variante D

En fait, les valeurs 1 à 40000 n'ont pas d'intérêt pour l'exercice en cours, c'est leur somme. Nous sélectionnons la cellule "C3" et modifions la formule y contenue comme suitl : '=SOMME(LIGNE(DECALER(A1;0;0;40000)))'.

A nouveau nous finissons la saisie avec "Ctrl"+"Maj"+"Valider" pour indiquer qu'il s'agit d'un calcul matriciel. Le résultat dans la cellule reste le même qu'avant, mais nous pouvons effacer complètement les valeurs de la colonne "A", la séquence étant générée directement dans la formule pour être sommée. Une sauvegarde du classeur montre : La séquence n'est pas stockque, le fichier implose à 8 KO!

Explication: La fonction LIGNE(DECALER(A1;0;0;40000)), saisie comme formule matricielle, renvoie une matrice à une colonne et 40000 lignes contenant les numéros des lignes 1 bis 40000 de la plage "A1:A40000". La somme en fait une seule valeur scalaire.

Applications

Filtre des sécuqences de données périodiques

Pour notre prochain exemple, nous nous servons des moyennes mensuelles des temperatures pour Payerne de MétéoSuisse, que nous collons dans les colonnes "A" à "D" comme présenté dans la copie d'écran suivante :

Nous souhaitons calculer les moyennes mensuelles sur toutes les années de l'horison des donnée. Comme exercice, nous réproduisons d'abord, dans les colonnes "F" et "G", les séquence des années et des mois.   Übung reproduzieren wir zunächst die Folgen der Jahre und Monate in den Spalten F und G, wobei wir das Anfangsjahr aus Zelle "A2" und den ersten Monat aus Zelle "C2" verwenden. Dazu sehen wir in den Spalten "F" und "G" einen Bereich für die Startwerte, die Grössenbestimmung und Konstanten vor:

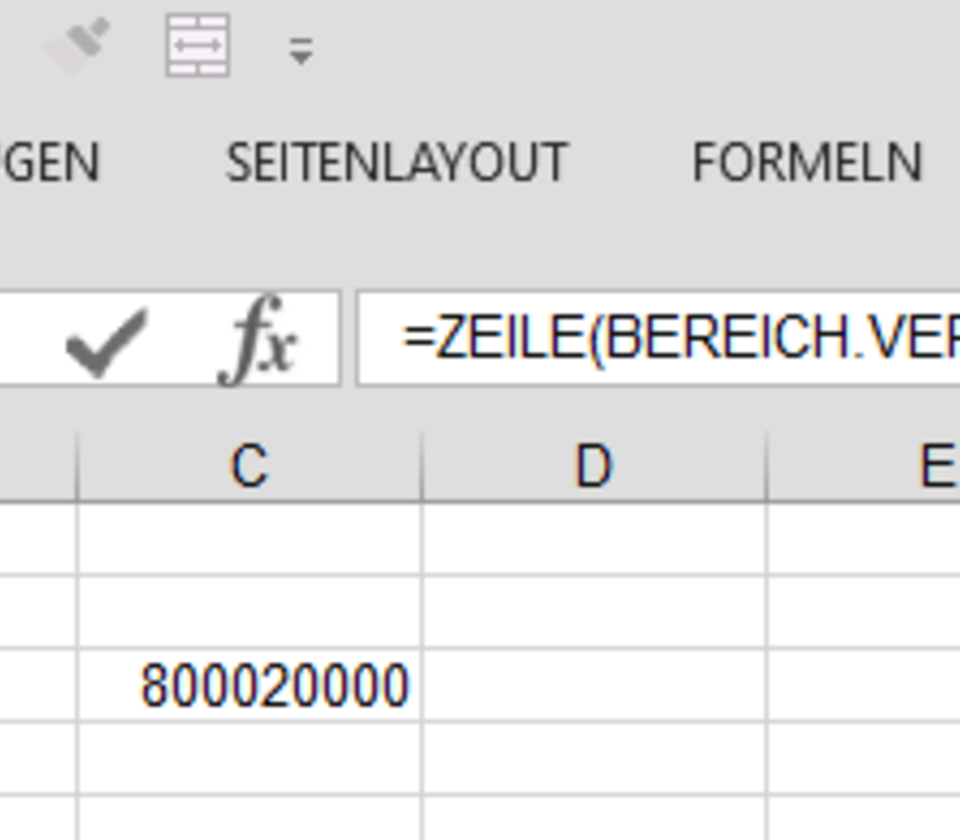
Die Formel für die Monate verwendet die Folge der Zahlen 1 bis n aus der Funktinon 'ZEILE(BEREICH.VERSCHIEBEN(A1;0;0;G3))' über einen Bereich, dessen Höhe durch die Anzahl Datenpunkte in "G3" bestimmt ist. Weil der erste Monat nicht die Nummer 1 trägt, müssen wir den Monat der ersten Datenzeile berücksichtigen:

'{=$G$6+GANZZAHL((ZEILE(BEREICH.VERSCHIEBEN(A1;0;0;G3))+$G$7-2)/G$5)}'

Nach je 12 Zeilen nimmt die Jahreszahl um 1 zu. Der Dividend 12 wird aber nicht als fester Wert in die Formel eingetragen, sondern als Konstante ab Zelle "G5" abgelesen. Damit lässt sich die Formel auch für ähnliche Anwendungen mit anderen Perioden verwenden.

Die Formel wird auf ein paar Zellen der Spalte "H" als Matrixformel eingegeben und dient nur zur Illustration und Kontrolle, ob die Ergebnisse den Monatsnummern aus den Originaldaten entsprechen.

Analog wird in Spalte "I" zur Kontrolle die Monatsnummer berechnet:

'{=REST(G7+ZEILE(BEREICH.VERSCHIEBEN(A1;0;0;G3))-2;$G$5)+1}'

Die Berechnung der Monatsmittelwerte für alle Monate leiten wir in drei Schritten her aus:

1. Anzahl Werten, die dem Kriterium entsprechen
2. Summe der Werte, die dem Kriterium entsprechen
3. Quotient von 2 und 1

Für das Zählen von Werten, die einem Kriterium entsprechen, verwenden wir den Abfrageausdruck '1*(Wert=Kriterium)'. Dieser Ausdruck liefert 1, wenn die Abfrage 'Wert=Kriterium' gleich ist, sonst 0. Als Wert verwenden wir die Matrixformel für die Monatszahlen, und als Kriterium den betreffenden Monat. Wir bereiten einen Datenbereich mit 12 Zeilen vor, in dessen erste Spalte "L" die Zahlen 1 bis 12 stehen:

In Spalte "M" fügen wir beim ersten Monat (in Zelle "M3") die Formel ein, die die Monatszahlen aus der Matrizenformel mit der Monatszahl vergleicht und für jede Übereinstimmung 1 liefert. Somit brauchen wir diese Matrizenformel nur noch zu summieren, um die Anzahl zu erhalten. Die Matrizenformel für die Monatszahlen befindet sich in Spalte "I", von wo wir sie direkt übernehmen können:

{=SUMME(1*(REST(G$7+ZEILE(BEREICH.VERSCHIEBEN($A$1;0;0;G$3))-2;G$5)+1=L3))}

En appliquant des "$" pour fixer des références aux lignes à "G3" et "G7", nous pouvons appliquer la formule à tous les mois en l'étirant. Le calcul de la somme se passe maintenant sans référence à une colonne auxiliaire contenant les mois.

La somme des valeurs mensuelles des mois respectifs est obtenue directement à partir de la formule de colonne "l" en remplaçant le facteur "1" par la liste des valeurs mensuelles :

{=SOMME(DECALER($C$2;0;0;G$3)*(RESTE(G$7+LIGNE(DECALER($A$1;0;0;G$3))-2;G$5)+1=L3))}

Nous pouvons exprimer la moyenne en tant que quotient de la somme par le nombre :

SOMME((RESTE(G$7+LIGNE(DECALER($A$1;0;0;G$3))-2;G$5)+1=L3)*DECALER($C$2;0;0;G$3))/SOMME(1*(RESTE(G$7+LIGNE(DECALER($A$1;0;0;G$3))-2;G$5)+1=L3))

Est expression dispose d'une belle longueur, mais elle nous permet de calculer les moyennes sans avoir besoin des mois et les années. DAns cet exemple nous économisons (pouvons ignorer ou supprimer) 600 valeurs, si des valeurs quart-horaires d'une année sont à sommer, 35000 lignes sont concernées, ce qui commence à peser si on peut se passer de quatre colonnes auxiliaires.

Moyennes par critère

L'expression que nous avons construite pour le calcul des années en colonnne "H"lt haben, nous sert maintenant pour obtenir les moyennes des températures mensuelles pour chaqueannée. Nous préparons une plage de données contenant dans la cellule "Q2" la première année et les suivantes en colonne vers le bas.

Pour vérification nous faisons le comptage des valeurs présentes pour chaque année :

{=SOMME(1*(G$6+ENTIER((LIGNE(DECALER($A$1;0;0;G$3))+G$7-2)/G$5)=Q2))}

Pour nous exercer, nous calculons en colonne "S" la somme des températures mensuelles de chaque anneé :

{=SOMME(DECALER(C$2;0;0;$G$3)*(G$6+ENTIER((LIGNE(DECALER($A$1;0;0;G$3))+G$7-2)/G$5)=Q2))}

Et pour bien finir, en colonne "T", les moyennes annuelles des températures mensuelles :

Ceux qui le souhaitent, peuvent se faire afficher l'évolution au fil des années en graphique :