Excel und Matrixformeln

Matrix formulas - first exercises

A simple exercise: Sum values from 1 to n

To demonstrate the efficiency of matrix formulas we want to sum the numbers form 1 to n. Of course, we could achieve this by using the expression n·(n+1)/2 but today we want to know what matrix formulas can do for us.

Variant A

First we use the formula '=ROW()' in column "A" to generate the sequence of natural numbers from 1 to 40'000. In cell "C3" we obtain the sum of these numbers by using a reference to the range '=SUM(OFFSET(A1;0;0;40000))'

We save the workbook and note its file size of about 442 KB in Office 2016.

Variant B

If we replace the formulas in column "A" by their values and save the workbook undder a different name, we note a file size reduction to 333 KB

Variant C

We generate the values from 1 to 40000 using a matrix formula in column "A". We select the range containing the current values (A1:A40000, that is) and enter into the formula field: '=ROW(OFFSET(A1;0;0;40000))'

We finish entry by pressing "Ctrl"+"Shift"+"Enter" to designate the expression as a matrix calculation. By selecting any of the cells covered by the expression, the formula is shown in curled braces: '{=ROW(OFFSET(A1;0;0;40000))}'. The file size of this workbook saved is close to that from variant "A".

Variant D

Now the numbers 1 to 40000 are of no interest to us, we just want to obtain their sum. We select cell "C3" and modify the existing formula to: '=SUM(ROW(OFFSET(A1;0;0;40000)))'.

Again we enter by "Ctrl"+"Shift"+"Enter" to obtain a matrix formula. The result remains the same, but we may now completely delete the values from column "A". The number sequence is now generated directly by the formula and immediately summed. Saving the workbook shows: No sequence is saved or stored, the workbook shrinks to a light 8 KB!

Explanation: The function ROW(OFFSET(A1;0;0;40000)), entered as matrix formula, returns the row numbers 1 to 40000 of the range "A1:A40000" as a one-column matrix. The sum then returns the sum as a single scalar value.

Use

Filtering periodic Data

For our example we take the monthly average temperatures for Payerne from MeteoSwiss and paste the data to columns "A" to "D" as indicated in the screen copyt:

Now we'd like to get the monhly averages over all years for all months of the year. Als Übung reproduzieren wir zunächst die Folgen der Jahre und Monate in den Spalten "F" und "G", wobei wir das Anfangsjahr aus Zelle "A2" und den ersten Monat aus Zelle "C2" verwenden. Dazu sehen wir in den Spalten "F" und "G" einen Bereich für die Startwerte, die Grössenbestimmung und Konstanten vor:

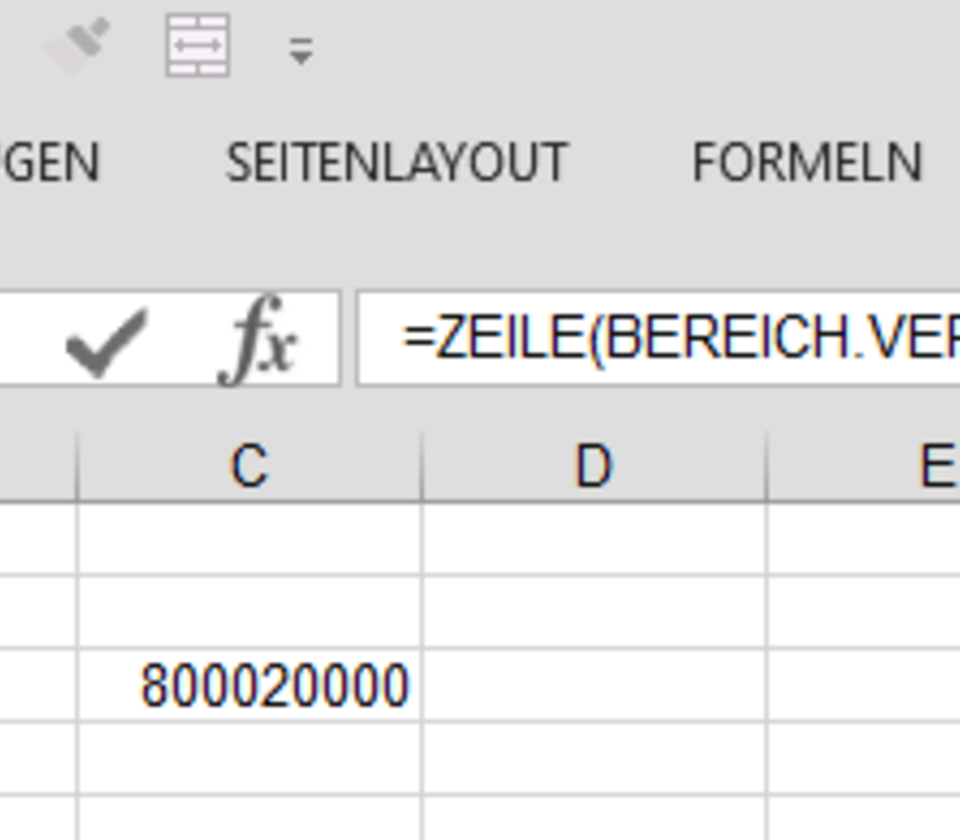
Die Formel für die Monate verwendet die Folge der Zahlen 1 bis n aus der Funktinon 'ZEILE(BEREICH.VERSCHIEBEN(A1;0;0;G3))' über einen Bereich, dessen Höhe durch die Anzahl Datenpunkte in "G3" bestimmt ist. Weil der erste Monat nicht die Nummer 1 trägt, müssen wir den Monat der ersten Datenzeile berücksichtigen:

'{=$G$6+GANZZAHL((ZEILE(BEREICH.VERSCHIEBEN(A1;0;0;G3))+$G$7-2)/G$5)}'

Nach je 12 Zeilen nimmt die Jahreszahl um 1 zu. Der Dividend 12 wird aber nicht als fester Wert in die Formel eingetragen, sondern als Konstante ab Zelle "G5" abgelesen. Damit lässt sich die Formel auch für ähnliche Anwendungen mit anderen Perioden verwenden.

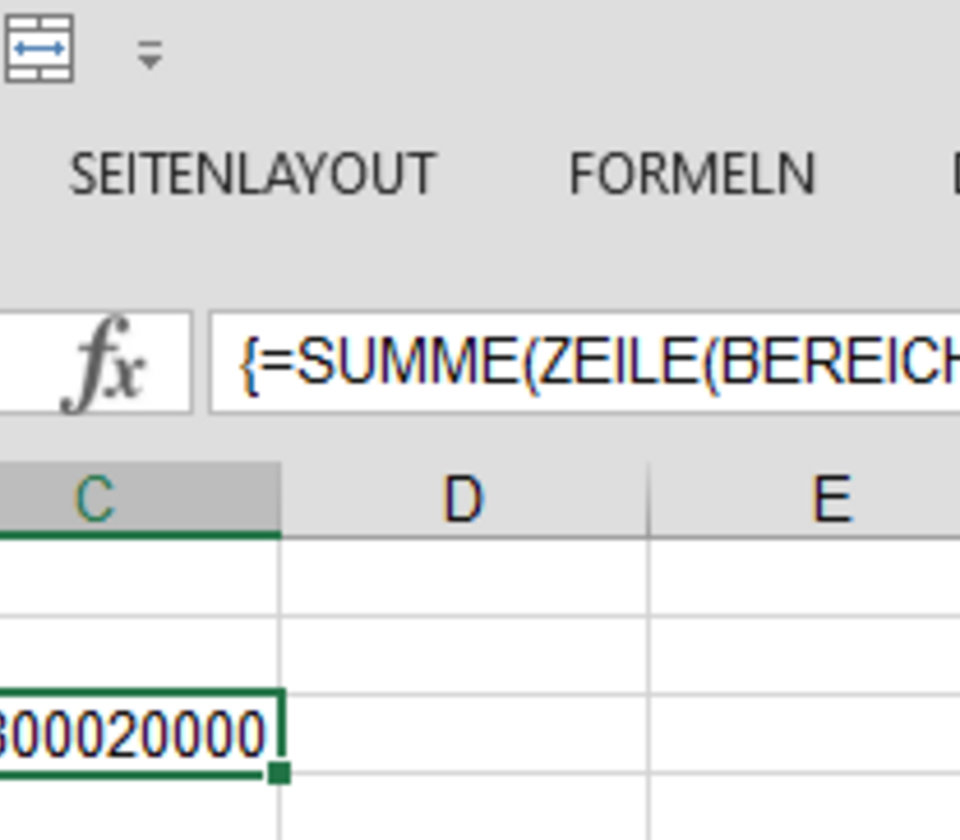
Die Formel wird auf ein paar Zellen der Spalte "H" als Matrixformel eingegeben und dient nur zur Illustration und Kontrolle, ob die Ergebnisse den Monatsnummern aus den Originaldaten entsprechen.

In analog manner we calculate the month number in column "I":

'{=REMAINDER(G7+ROW(OFFSET(A1;0;0;G3))-2;$G$5)+1}'

We derive the calculation of the averages in three steps:

1. Count the values matching the criterion
2. Sum the values matching the criterion
3. Quotient of 2 by 1

To count the values matching a condition, we express the comparison as '1*(Value=criterion)'. This expression returns 1 for a match and 0 othersise. For the value list we use the matrix formula for the month numbers and as the criteria we use the corresponding month. We prepare a data range with 12 rows and put the values from 1 to 12 in its first column ("L"):

In column "M" we enter in Zelle "M3" the formula comparing the month number sequence from the matrix formula with the month number in column "L", returning 1 for every match. So we just need to sum this list to get the count. The matrix formula for the month numbers is contained in column "I" from where we can re-use it directyl:

{=SUM(1*(MOD(G$7+ROW(OFFSET($A$1;0;0;G$3))-2;G$5)+1=L3))}

Setting the right blocks for row references to "G3"aund "G7" we can now apply this formula to all subsequent months by dragging the formula down to the last month. The sum of the monthly values now no longer refers to any auxiliary column containing the month numbers in the data.

Die Summe der Monatswerte der betreffenden Monate erstellen wir direkt aus der Formel für die Anzahl, indem wir die "1" ersetzen durch die Liste der Monatswerte:

{=SUMME(BEREICH.VERSCHIEBEN($C$2;0;0;G$3)*(REST(G$7+ZEILE(BEREICH.VERSCHIEBEN($A$1;0;0;G$3))-2;G$5)+1=L3))}

Die Mittelung können wir nun als Quotient der Wertesumme durch die Werteanzahl ausdrücken:

SUMME((REST(G$7+ZEILE(BEREICH.VERSCHIEBEN($A$1;0;0;G$3))-2;G$5)+1=L3)*BEREICH.VERSCHIEBEN($C$2;0;0;G$3))/SUMME(1*(REST(G$7+ZEILE(BEREICH.VERSCHIEBEN($A$1;0;0;G$3))-2;G$5)+1=L3))

Dies ist zwar ein ordentlich langer Ausdruck, er erlaubt uns aber, die Mittelwerte ohne die Monats- und Jahreszahlen zu berechnen. In diesem Beispiel können wir je 600 Werte einsparen, bei Summen von Viertelsundenwerten über ein Jahr sind es 35000, was bei drei bis vier Hilfsspalten langsam ins Gewicht fällt.

Averaging over criteria

The expression we assembled to calculated the year numbers in column "H" now serves to obtain the annual average of the monthly temperatures. Again we prepare a data range containing in cell "Q2" the first year and the subsequent ones in the column downwards.

To verify we first count the values presen for each year:

{=SUM(1*(G$6+INT((ROW(OFFSET($A$1;0;0;G$3))+G$7-2)/G$5)=Q2))}

As a little exercise we calculate the yearly sum of the monhly values in column "S" for the corresponding year:

{=SUM(OFFSET(C$2;0;0;$G$3)*(G$6+INT((ROW(OFFSET($A$1;0;0;G$3))+G$7-2)/G$5)=Q2))}

Last but no least the yearly averages in column "T":

Those who are interested may have output the evolution over the years as a graph: