Apollonisches Berührungsproblem - Kreise

Trois objets en plaine

Etant donné trois objets en plaine, on cherche tous les cercles tangeants à chacun des objets. Les objets sont des cercles généralisé, incluant les droites et les points.

Pour les cas de trois points et trois cercles, le classeur Excel présenté montre la dérivation de la solution agébrique ainsi que la représentation graphique 2D de la solution.

Solution algébrique - PPP (trois points)

Etant donné trois points, la solution, définie par les coordonnées du centre (x_s,y_s) et le rayon r_s du cercle solution, sort de la condition que la distance du centre (x_s,y_s) des trois points (x_i,y_i) soit égale à r_s. La dérivation de la solution algébrique est contenue dans le classeur Excel pour le cas général. Il en sort le cercle circonscripteur du triangle entre les trois points. On pourrait alors construire le centre de la solution de manière géométrique, nous y renonçons.

Un cas spécial est donné si les trois points sont collinéaires. La solution est la droit passant aux trois points - un cercle de rayon infini.

Quand deux points coïncident, le nombre de solutions est infini. Les centres de ces cercles se situent sur le bisecteur perpendiculier entre deux points distincts.

Solution algébrique - CCC (trois cercles)

Etant donné trois cercles, l'insertion de la relation de x_s et y_s de r_s dans une des conditions initiales produit une équation quadratique en r_s et alors une ou deux solutions possibles. En écartant les valeurs négatives de r_s le jeu des solutions est effectivement confiné.

Etant donné trois cercles, en fonction de leur constellation il existent jusqu'à 8 combinaisons pour la solution d'inclure ou exclure les cercles données. Si les trois cercles sont disjoints, chaque solution correspond à une condition initiale. Quand les cercles font des sections, il faut considérer les deux valeurs r_s de l'équation quadratique pour chaque combinaison.

Classeur Excel

Feuille PPP

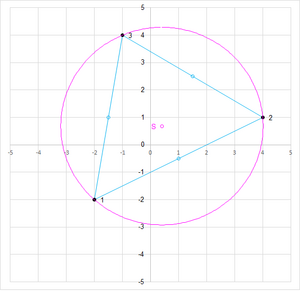
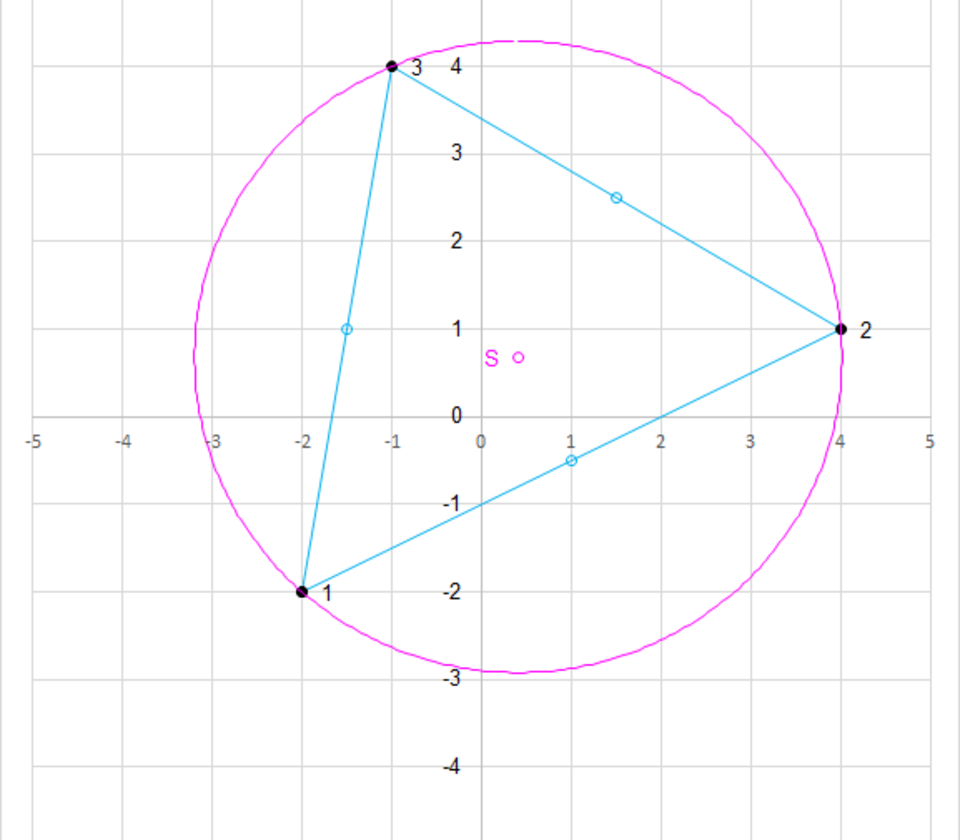
Montre la dérivation de la solution algébrique et la représentation graphique des trois points et de la solutionene. Egalement il montre les côtés triangulaires et leur bisecteurs.

Feuille CCC

Montre la dérivation de la solution algébrique ainsi que deux représentations graphiques.

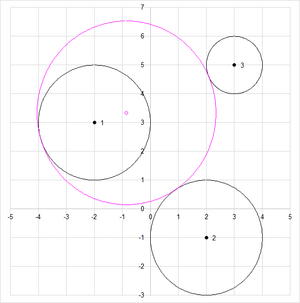
Le graphique gauche montre la solution pour une combinaison spécifique d'inclusion et d'exclusion des cercles donnés par la solution.

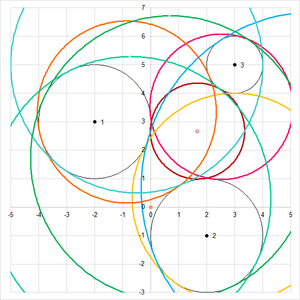
Le graphique à droite montre tous les cercles de solutions ensembles.

Cas spéciaux

Si la solution est une ligne droite, elle n'est pas trouvée par le calcul dans la feuille.

La feuille ignore tous les cas avec des droites. Ces cas sont de catégorie "L" et seront traités à part dans des versions ultérieures.