Kreisberührung
Gegeben sind drei Objekte in der Ebene. Gesucht sind alle Kreise, die jedes dieser Objekte berühren. Die Objekte sind verallgemeinerte Kreise, d.h. auch Punkte und Geraden. Eine sehr schöne Abhandlung ist in einer Publikation der Uni Wuppertal zu finden.
Für die Fälle von drei Punkten und drei Kreisen zeigt die Excel-Arbeitsmappe die algebraische Lösung und ihre Darstellung als 2D-Grafik.
Algebraische Lösung - PPP (drei Punkte)
Bei drei gegebenen Punkten ergibt sich der Lösungskreis, definiert durch die X- und Y-Koordinate seines Zentrums (xs,ys) sowie seinen Radius rs, aus der Bedingung, dass für jeden gegebenen Punkt (xi,yi) den Abstand zum Zentrum (xs,ys) gleich rs sei. Die Excel-Arbeitsmappe enthält die Auflösung des Gleichungssystems für den allgemeinen Fall. Es ergibt sich der Umkreis des Dreiecks zwischen den drei gegebenen Punkten. Das Zentrum könnte also auch über die Mittelsenkrechten auf den der Dreiecksseiten konstruiert werden, was in der Excel-Mappe jedoch nicht ausgeführt ist.
Spezialfälle ergeben sich , wenn die drei Punkte kollinear sind, d.h. auf einer Geraden liegen. Dann ist die Lösung die Gerade durch die drei Punkte - ein Kreis mit Radius unendlich.
Wenn zwei Punkte zusammenfallen, ergeben sich unendlich viele Lösungen. Die Zentren dieser Kreise liegen auf der Mittelsenkrechten zwischen zwei unterscheidbaren Punkten.
Algebraische Lösung - CCC (Drei Kreise)
Sind drei Kreise gegeben, so liefert die Einsetzung der Beziehung für xs und ys aus rs in eine der Anfangsgleichungen eine quadratische Gleichung in rs und somit mehrere mögliche Lösungen. Durch Ausschluss negativer rs wird die Lösungsmenge effektiv auf die unterscheidbaren Lösungen eingegrenzt.
Sind drei Kreise gegeben, so ergeben sich für den Lösungskreis - je nach Konstellation - bis zu 8 verschiedene Kombinationen, die drei Kreise ein- oder auszuschliessen. Wenn sich die drei Kreise nicht berühren oder überschneiden, so entspricht jede Kombination einer anderen Anfangsbedingung. Bei überschneidenden Kreisen sind die Verhältnisse komplizierter, und es müssen jeweils beide Lösungen der quadratischen Gleichung betrachtet werden.
Excel-Arbeitsmappe
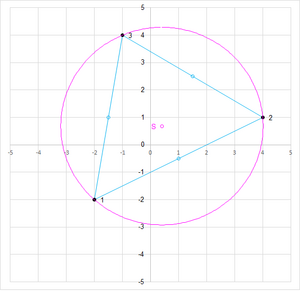
Blatt PPP
Zeigt die Herleitung der Lösung und die grafische Darstellung für drei vorgegebene Punkte sowie die Seiten des Dreiecks zwischen den Punkten und deren Mittelpunkten.
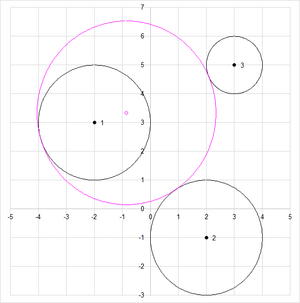
Blatt CCC
Zeigt die Herleitung der Lösung und zwei grafische Darstellungen.
Die linke Grafik zeigt den Lösungskreis für die eingestellte Auswahl an Ein- und Ausschliessung für den Lösungskreis zu den vorgegebenen Punkten.
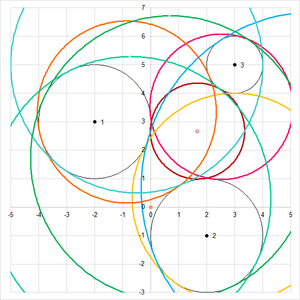
Die rechte Grafik zeigt alle Lösungskreise zusammen.
Spezialfälle
Wenn die Lösung eine Tangente an alle drei Kreise ist, kann die Berechnung der Mappe sie nicht finden.
Ebenfalls nicht behandelt sind in diesem Blatt sämtliche Fälle mit gegebenen Geraden. Diese stellen ohnehin Fälle der Kategorien "L" dar und werden in späteren Versionen gesondert behandelt.




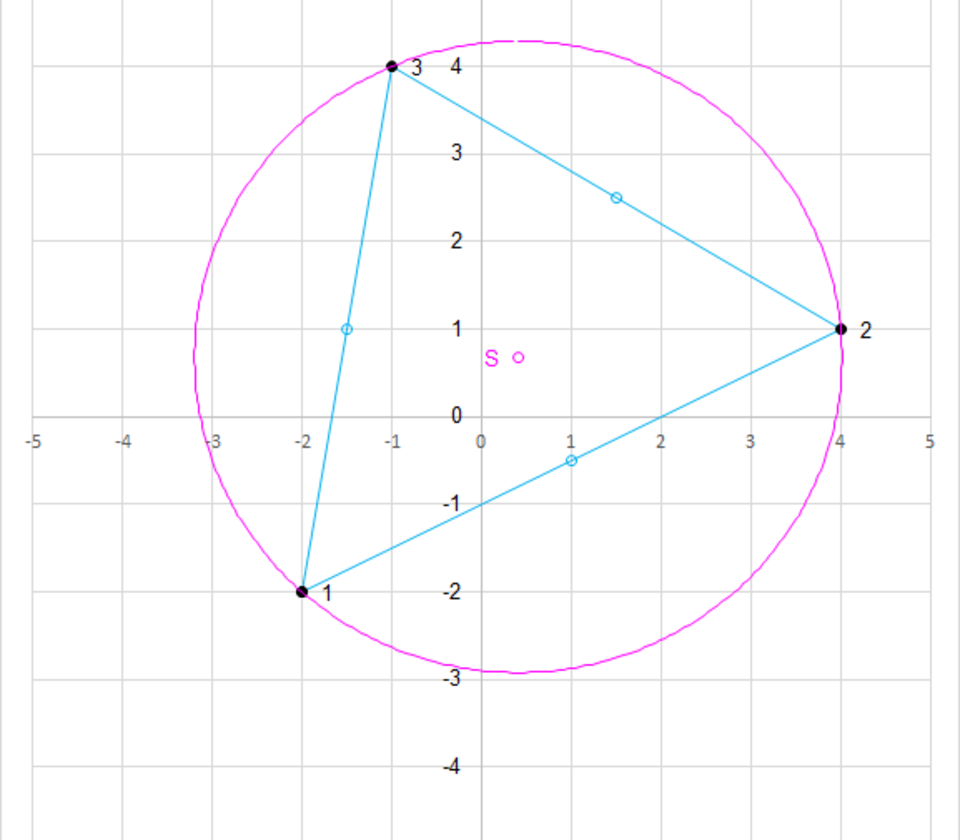
Sei der erste der kommentiert