Statische Berechnungen von Stabwerken

Statik von Stabwerken

Ein Stabwerk ist bestimmt durch die Ortsvektoren einer Anzahl NK Knoten und einer Anzahl NS gerader Stäbe zwischen zwei je Knoten. Die Stäbe besitzen eine Masse und Lastkräfte greifen in den Knoten an. Das Stabwerk ist in zwei Punkten aufgelagert. Bei der Auflagerung gibt es zwei Fälle:

1. Das standfeste Stabwerk, bei eine steife Verbindung zwischen den Auflagerknoten besteht. Damit dieses Stabwerk statisch bestimmt ist, muss eine Bedingung gelockert werden. Dies erfolgt durch Auflagerung auf einem Gleitlager. Dieses ist durch die Vorgabe des Normalenvektors zur Auflagerebene definiert.
2. Das Pendelstützen-Stabwerk, welches zwei feste Lager benötigt

Formale Problemdefinition

Gegeben sind eine Anzahl Nk Knoten und eine Anzahl Stäbe sowie zwei Knoten, für welche die Lagerkräfte gesucht sind. Jeder Stab verursacht an seinen Enden Schwerkräfte in den entsprechenden Knoten. In den Knoten greifen Lastkräfte an. Alle Kräfte sind als zweikomponentige Vektoren notiert, alternativ und gleichwertig auch Richtungswinkel und Vektorbetrag

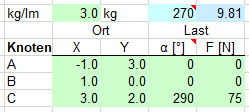
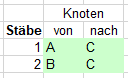
Gesucht sind:

1. Skalare der Kraftbeträge für die Stabkraft eines jeden Stabes
2. Kraftvektor der Auflagerkraft im Auflager A
3. im Auflager B
   1. Skalar des Kraftbetrages für die Auflagerkaft entang des Normalenvektors bei standfestem Stabwerk
   2. Kraftvektor der Auflagerkraft im Auflager B im anderen Fall

Nebenbedingungen

Da sich die Knoten nicht bewegen, ist die Summe aller Kräfte in jedem Koten gleich Null

Da sich die Stäbe nicht bewegen, ist die Summe der Kräfte in jedem Stab gleich Null

Da sich das Stabwerk als Ganzes nicht bewegt, ist die Summe aller Schwer- und Lastkräfte und der Auflagerkräfte in A und B gleich Null

Gleichungssystem

Das Gleichungssystem legt die Gleichgewichtsbedingung für jede Komponente des Kraftvektors in jedem Knoten fest, enthält somit 2 NK Gleichungen in ebensovielen Zeilen

Für den Fall eines standfesten Stabwerks ergeben sich folgende Unbekannte:

1. NS Skalare für die Stabkraft-Beträge
2. 2 Komponenten der Lagerkraft A
3. 1 Skalar für den Betrag der Lagerkraft B

Damit gibt es eine Bedingung für die Anzahl Stäbe in einem solchen Stabwerk: NS = 2NK - 3

Im Falle eines nicht standfesten Systems ergeben sich folgende Unbekannte

1. NS Skalare für die Stabkraft-Beträge
2. 2 Komponenten der Lagerkraft A
3. 2 Komponenten der Lagerkraft B

Und für diesen Fall also ist die Anzahl Stäbe: NS = 2NK - 4

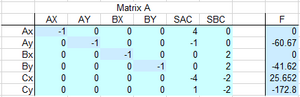
Wenn dieses aufgelöst werden kann, d.h. die Determinante der Matrix A nicht Null ist, so enthält der Lösungsvektor alle gesuchten Elemente:

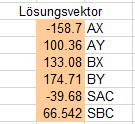
Ausgewertet auf die Knoten und Stäbe ergibt sich das Kräftediagramm:

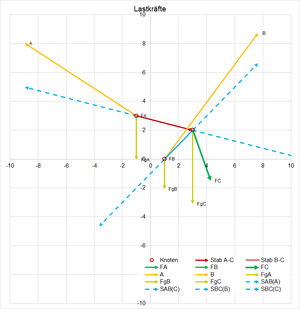
Analyse-Werkzeug

QRS hat ein Excel-Werkzeug entwickelt, mit dem ein Stabwerk auf einfache Weise analysiert werden kann. Die Abbildungen stammen aus dem Arbeitsblatt für ein Stabwerk mit drei Knoten und drei Stäben. Die aktuelle Version erlaubt 10 Knoten und maximal 16 oder 17 Stäbe. Der Winkel der Schwerkraft kann (für alle Schwerkräfte) beliebig angegeben werden.

Literatur:

Löwe, Harald; Statik von Fachwerken; TU Braunschweig, Institut for computational mathematics, D-38106 Braunschweig, Deutschland

Wandinger, Johannes; Einfache ebene Tragwerke; Hochschule München