Kubische Kurve durch zwei Punkte - Matrixnotation

Gleichungssystem und Matrizen

Dieser Artikel setzt fort, was unter dem Titel "Kubische Kurve durch zwei Punkte" bereits eingeführt wurde.

Die Gleichungen, die zur Bestimmung de Koeffizienten aufzustellen sind, lassen sich auch als Matrizen aufschreiben. Dabei werden die Matrizen aus den Bedingungen heraus erstellt.

Ac = b

Gegeben ist der Vektor b der Bedingungen. Bei einer Kurve durch zwei Punkte, in denen die Steigung jeweils gegeben ist, lautet b: [y₀, y₁, m₀, m₁]

Ferner sind natürlich x₀ und x₁ gegeben und somit kann man zwei Vektoren v₀ = [1, x₀, x₀², x₀³] und v₁ = [1, x₁, x₁², x₁³] angeben, die zur Verwendung in der Matrix A dienen:

A₁ = v₀ (erste Zeile)

A₂ = v₁ (zweite Zeile)

A₃ = [0, 1v₀₁, 2v₀₂, 3v₀₃] (dritte Zeile)

A₄ = [0, 1v₁₁, 2v₁₂, 3v₁₃] (vierte Zeile)

Aus dieser Matrix kann die Inverse bestimmt werden, und man erhält den Koeffizientenvektor c durch die Multiplikation A^-1b

Beispiel

Die nachstehende Abbildung zeigt eine Beispielrechnung in Excel

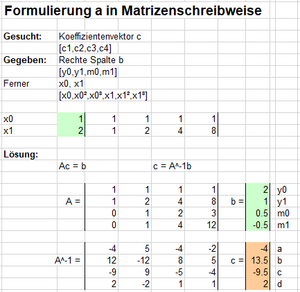
Das Schmankerl: Gegebene Fläche unter der Kurve

Für gewisse Anwendungen kann es notwendig sein, als Bedingung die Fläche unter der Kurve zwischen den beiden Endpunkten anzugeben. Dies kann durch Integration der Polynomfunktion einfach formuliert werden:

F = ax + b/2x² + c/3x³ + d/4x⁴, bzw.

F = a(x₁ - x₀) + b(x₁² - x₀²)/2 + c(x₁³ - x₀³)/3 + d(x₁⁴ - x₀⁴)/4

Dadurch bleibt eine einzelne Bedingung übrig, die noch gewählt werden kann.