Worum geht's?
Die Berechnung von Splinekurven erfordert die Lösung von Gleichungssystemen, wobei die Anzahl Gleichungen nahe der Anzahl Stützstellen liegt. Für kubische Splines sind die Matrizen der entsprechenden Gleichungssysteme nur entlang der Diagonalen sowie beiderseitss je einer Nebendiagonalen besetzt. Für diese Gleichungssysteme gibt es bekannte einfache Lösungen.
Für Splinefunktionen höherer Ordnung oder andere Randwertprobleme kann es nützlich sein, Gleichungssysteme mit je zwei Nebendiagonalen lösen zu können. Eine solche Lösung wird im Folgenden hergeleitet und gezeigt.
LR-Zerlegung
Die Lösung des Gleichungssystems beruht auf der LU-Zerlegung und der Tatsache - der Beweis sei hier unterlassen - dass die LU-Zerlegung eine Bandmatrix wieder eine Bandmatrix derselben Breite ist.
Gehen wir von der Ausgangsmatrix A mit 2-2-Bandstruktur aus und betrachten die beiden ersten Schritte der LR-Zerlegung:
1. Schritt
Der erste Schritt macht aus der Matrix A = A(1) die Matrix A(2)

Welche Elemente werden wie verändert?
- Die 1. Zeile bleibt unverändert
- Die 1. Spalte ab Zeile 2 entsteht durch Division der Elemente a21...an1 durch a11, wobei wegen der Bandstruktur nur a21 und a31 von Belang sind, die anderen sind Null
- Die Untermatrix a(2)22 bis a(2)33 entsteht durch das Subtraktion des dyadischen Vektorprodukts der Vektoren [a(2)21, a(2)31]T mit [a(1)12, a(1)13] von [[a(1)22, a(1)23], [a(1)32, a(1)33]]
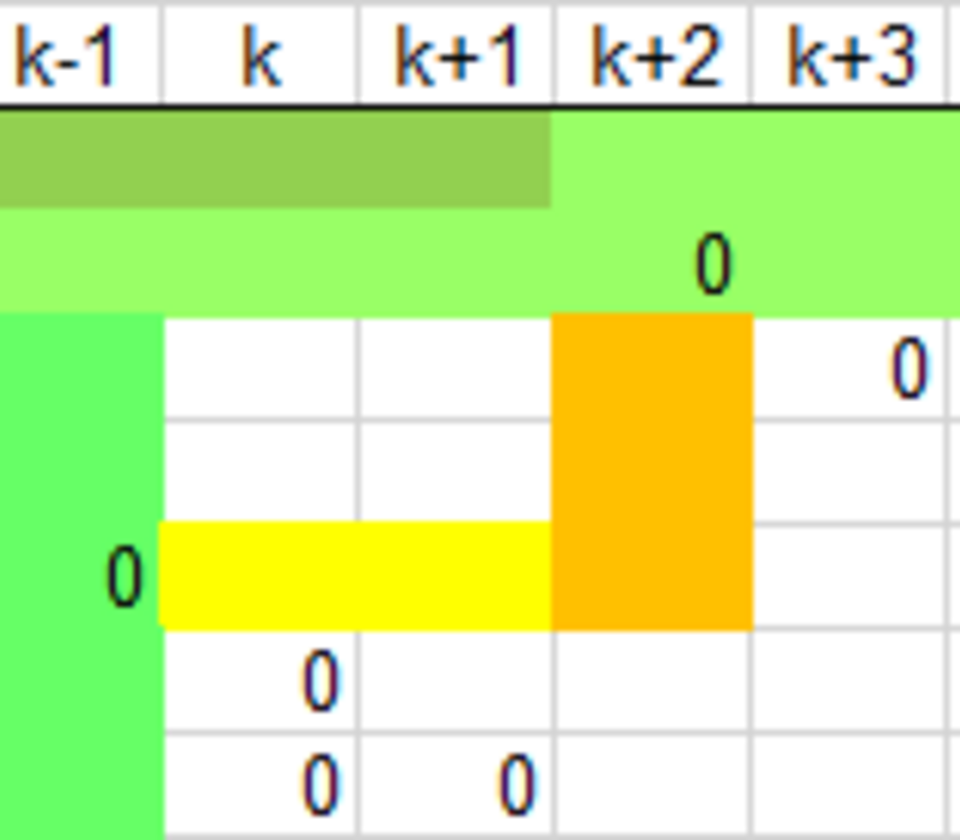
a(2)22 = a(1)22 – (a(1)12a(1)21)/a(1)11 usw. - Spalte 4, in der Grafik orange eingefärbt, entsteht ebenfalls aus Spalte 4 durch Subtraktion eines Produkts aus dem Vektor der Spalte 1 mit Zeile 1. Diese enthält jedoch Null, so bleiben Spalte 4 und alle folgenden unverändert.
- Analoges gilt für die Zeile 4, gelb eingefärbt, und weiter bis Zeile n
Alles in Allem werden also nur Elemente in der Untermatrix A(1)2..3,1..3 verändert.
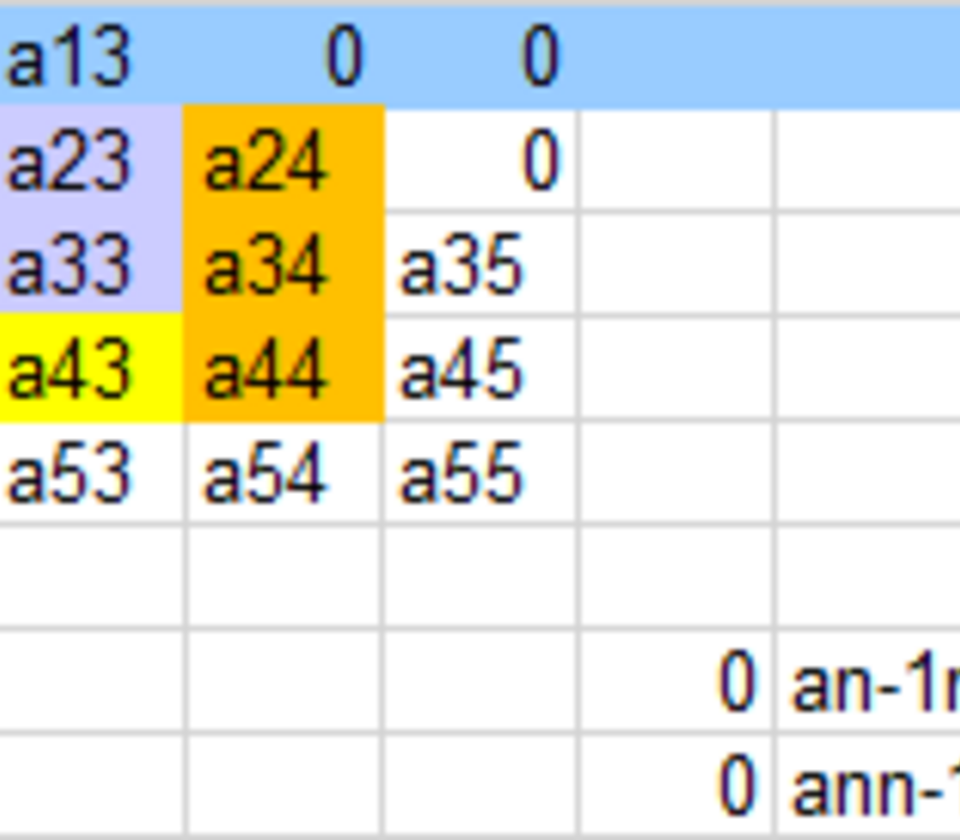
2. Schritt
Im 2. Schritt wird die Matrix A(2) in die Matrix A(3) überführt, und wieder werden nur die Elemente in einem 2x3-Block verändert.
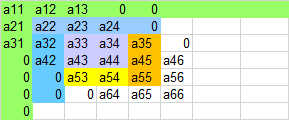
Welche Elemente werden wir verändert?
- Zeile 2 bleibt unverändert
- Spalte 2, Elemente a(3)32 und a(3)42 entstehen aus a(2)32 und a(2)42 durch Division mit a(2)22 aus dem 1. Schritt. Diese beiden Manipulationen müssen in einer Formel zusammengefasst werden: a(3)32 = (a(1)32 – (a(2)12a(2)31)/a(2)11)/a(2)22) usw.
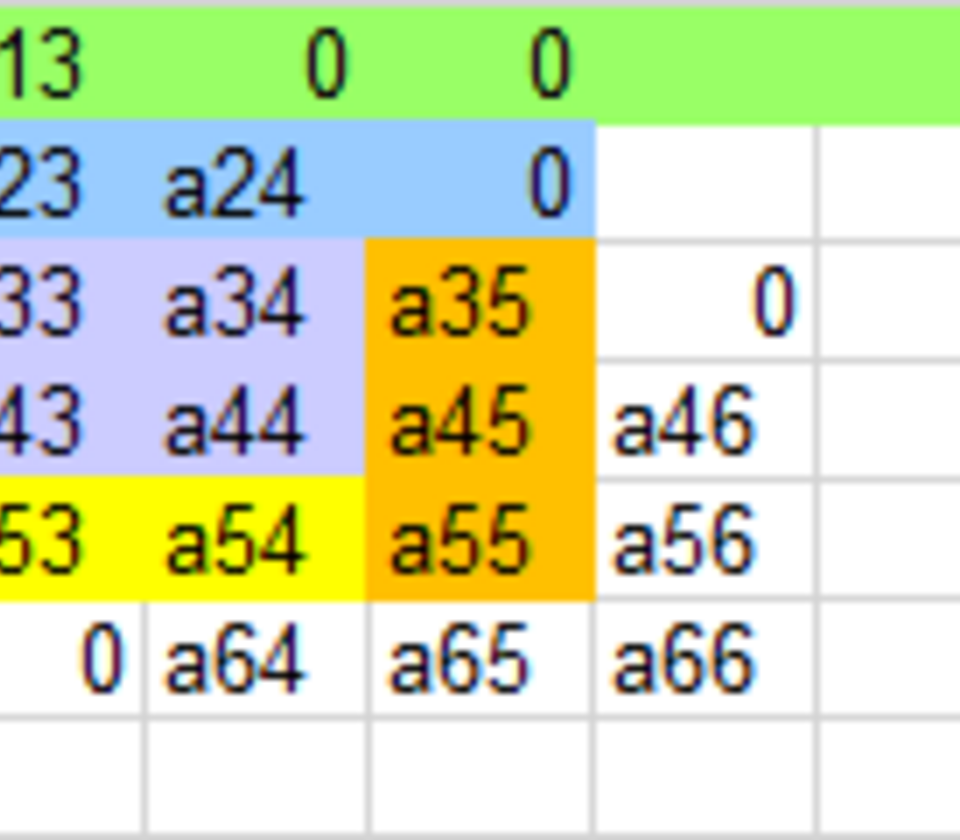
- Die Untermatrix a(3)33 bis a(3)44 entsteht durch Subtraktion des dyadischen Vektorprodukts der Vektoren [a(3)32, a(3)42]T mit [a(2)23, a(2)24] von [[a(2)33, a(2)34], [a(2)43, a(2)44]]
Davon ist speziell das Diagonalelement a(3)33 zu erwähnen, welches aus a(2)33 hervorgeht. Element a(2)33 kann nicht zwischengespeichert werden, und deshalb wird der Berechnungsschritt von a(1)33 nach a(2)33 auch in die Formel aufgenommen. Für die Elemente der 4. Zeile und 4. Spalte können die Eingangswerte aus der Originalmatrix verwendet werden
Für die weiteren Berechnungsschritte k liegen die Eingangswerte der Berechnungen entweder in A(k-1), d.h. im Bereich des Rechenschemas, oder in der Originalmatrix A vor.
Beispiel
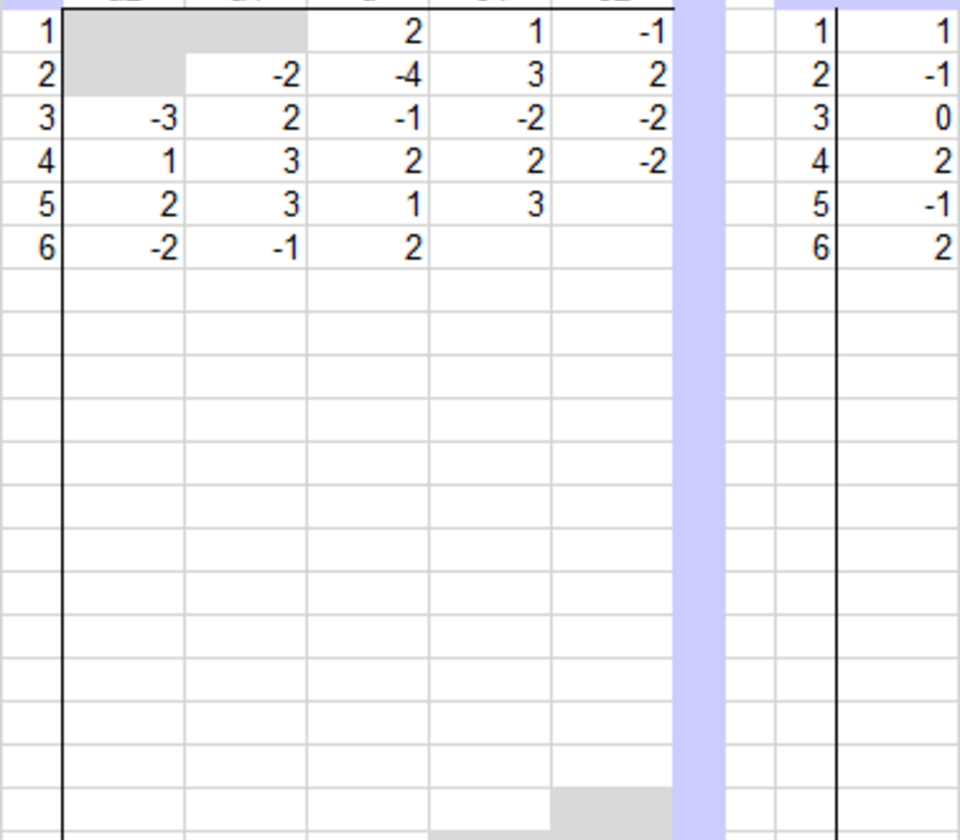
Gleichungssystem Ax - b = 0
Matrix A und Bedingungsvektor b
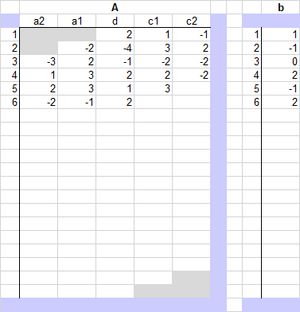
Das implementierte Rechenschema kann 20 Gleichungen verarbeiten, aber auch weniger. Es werden keine Pivotelemente gesucht. Im Eingangsbereich von A sind die Spalten a2 und a1 die unteren Nebendiagonalen, Spalten c1 und c2 die oberen.
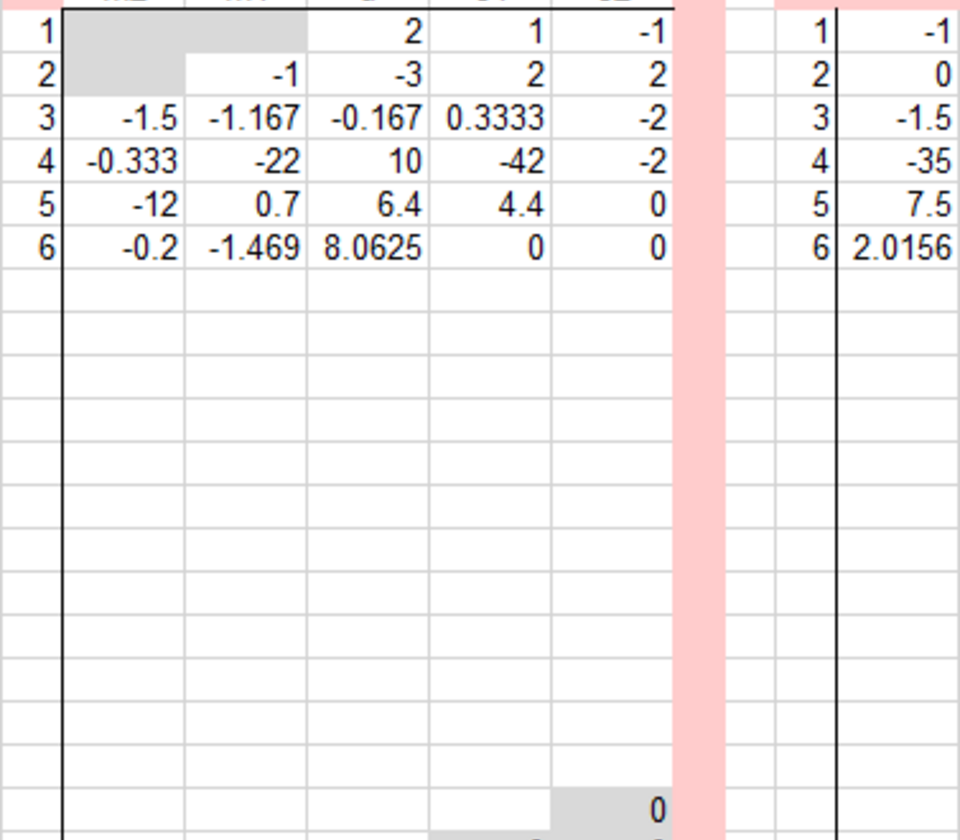
LR-Zerlegung und Vektor y
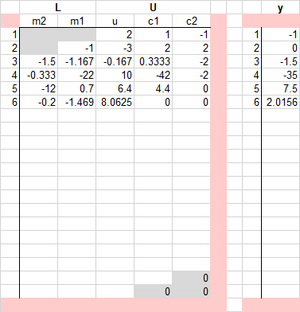
Die LR-Zerlegung von A in einem Format analog zur speichersparenden Zusammenlegung in der vollen Matrizenform: die L-Matrix, mit M bezeichnet, hat eine Diagonale mit lauter Einsen, die nicht gespeichert werden, sondern im Rechenschema eingesetzt sind.
Lösungsvektor x

Die Lösung des Gleichungssystems.


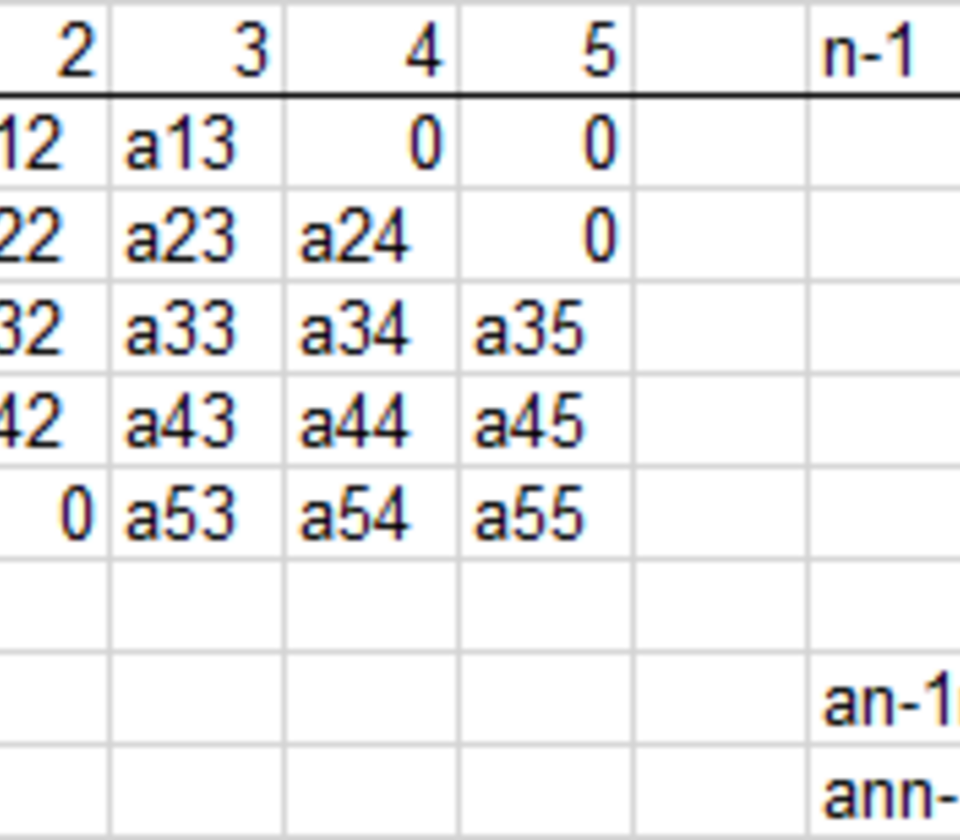

Sei der erste der kommentiert